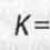Тэгшитгэлийн систем. Жишээ бүхий нарийвчилсан онол (2020). Энгийн шугаман тэгшитгэлийг шийдвэрлэх Тэгшитгэлийн төрөл, тэдгээрийг шийдвэрлэх арга

Таны хувийн нууцыг хадгалах нь бидний хувьд чухал юм. Энэ шалтгааны улмаас бид таны мэдээллийг хэрхэн ашиглах, хадгалах талаар тодорхойлсон Нууцлалын бодлогыг боловсруулсан. Манай нууцлалын практикийг хянаж үзээд асуух зүйл байвал бидэнд мэдэгдэнэ үү.

Хувийн мэдээллийг цуглуулах, ашиглах

Хувийн мэдээлэл гэдэг нь тодорхой хүнийг таних эсвэл холбоо барихад ашиглаж болох өгөгдлийг хэлнэ.

Та бидэнтэй холбоо барихдаа хүссэн үедээ хувийн мэдээллээ өгөхийг шаардаж болно.

Бидний цуглуулж болох хувийн мэдээллийн төрлүүд болон эдгээр мэдээллийг хэрхэн ашиглаж болох зарим жишээг доор харуулав.

Бид ямар хувийн мэдээллийг цуглуулдаг вэ:

• Таныг сайт дээр өргөдөл гаргах үед бид таны нэр, утасны дугаар, имэйл хаяг гэх мэт янз бүрийн мэдээллийг цуглуулж болно.

Бид таны хувийн мэдээллийг хэрхэн ашигладаг вэ:

• Бидний цуглуулсан хувийн мэдээлэл нь өвөрмөц санал, урамшуулал болон бусад арга хэмжээ, удахгүй болох арга хэмжээний талаар тантай холбогдох боломжийг олгодог.
• Бид үе үе таны хувийн мэдээллийг ашиглан чухал мэдэгдэл, харилцаа холбоог илгээж болно.
• Мөн бид үзүүлж буй үйлчилгээгээ сайжруулах, танд үйлчилгээнийхээ талаар зөвлөмж өгөх зорилгоор аудит хийх, мэдээллийн дүн шинжилгээ хийх, төрөл бүрийн судалгаа хийх зэрэг хувийн мэдээллийг дотоод зорилгоор ашиглаж болно.
• Хэрэв та шагналын сугалаа, уралдаан эсвэл үүнтэй төстэй сурталчилгаанд оролцсон бол бид таны өгсөн мэдээллийг ийм хөтөлбөрийг удирдахад ашиглаж болно.

Гуравдагч этгээдэд мэдээллийг задруулах

Бид танаас хүлээн авсан мэдээллийг гуравдагч этгээдэд задруулахгүй.

Үл хамаарах зүйл:

• Шаардлагатай бол - хууль тогтоомжийн дагуу, шүүхийн журмаар, шүүхийн журмаар, ба/эсвэл ОХУ-ын нутаг дэвсгэр дэх төрийн байгууллагуудын хүсэлт, хүсэлтийн үндсэн дээр хувийн мэдээллээ задруулах. Аюулгүй байдал, хууль сахиулах болон бусад олон нийтийн ач холбогдолтой зорилгоор ийм мэдээлэл шаардлагатай эсвэл тохиромжтой гэж үзвэл бид таны тухай мэдээллийг задруулах боломжтой.
• Дахин зохион байгуулалтад орох, нэгдэх, худалдах тохиолдолд бид цуглуулсан хувийн мэдээллээ холбогдох өв залгамжлагч гуравдагч этгээдэд шилжүүлж болно.

Хувийн мэдээллийг хамгаалах

Бид таны хувийн мэдээллийг алдах, хулгайлах, зүй бусаар ашиглах, зөвшөөрөлгүй нэвтрэх, задруулах, өөрчлөх, устгахаас хамгаалахын тулд захиргааны, техникийн болон биет байдлын зэрэг урьдчилан сэргийлэх арга хэмжээг авдаг.

Компанийн түвшинд таны хувийн нууцыг хүндэтгэх

Таны хувийн мэдээллийг найдвартай байлгахын тулд бид нууцлал, аюулгүй байдлын стандартыг ажилтнууддаа мэдээлж, нууцлалын практикийг чанд мөрддөг.

Шугаман тэгшитгэлнь алгебрийн тэгшитгэл юм. Энэ тэгшитгэлд түүнийг бүрдүүлэгч олон гишүүнтүүдийн нийт зэрэг нь нэгтэй тэнцүү байна.

Шугаман тэгшитгэлийг дараах байдлаар үзүүлэв.

Ерөнхий хэлбэрээр: а 1 x 1 + а 2 x 2 + … + a n x n + б = 0

Каноник хэлбэрээр: a 1 x 1 + a 2 x 2 + … + a n x n = b.

Нэг хувьсагчтай шугаман тэгшитгэл.

1 хувьсагчтай шугаман тэгшитгэлийг дараах хэлбэрт оруулав.

сүх+ б=0.

Жишээлбэл:

2х + 7 = 0. Хаана a=2, b=7;

0.1x - 2.3 = 0.Хаана a=0.1, b=-2.3;

12x + 1/2 = 0.Хаана a=12, b=1/2.

Үндэсний тоо нь үүнээс хамаарна аТэгээд б:

Хэзээ а= б=0 , энэ нь тэгшитгэл нь хязгааргүй тооны шийдтэй гэсэн үг, учир нь .

Хэзээ а=0 , б≠ 0 , учир нь тэгшитгэл нь үндэсгүй гэсэн үг.

Хэзээ а ≠ 0 , энэ нь тэгшитгэл нь зөвхөн нэг үндэстэй гэсэн үг юм.

Хоёр хувьсагчтай шугаман тэгшитгэл.

Хувьсагчтай тэгшитгэл xтөрлийн тэгш байдал юм A(x)=B(x), Хаана A(x)Тэгээд B(x)- илэрхийллүүд x. Багцыг орлуулах үед Түнэт зүйлс xТэгшитгэлд бид жинхэнэ тоон тэгшитгэлийг олж авдаг бөгөөд үүнийг нэрлэдэг үнэний багцэнэ тэгшитгэл ч гэсэн өгөгдсөн тэгшитгэлийн шийдэл, мөн хувьсагчийн ийм бүх утгууд нь байна тэгшитгэлийн үндэс.

2 хувьсагчийн шугаман тэгшитгэлийг дараах хэлбэрээр үзүүлэв.

Ерөнхий хэлбэрээр: ax + by + c = 0,

Каноник хэлбэрээр: ax + by = -c,

Шугаман функц хэлбэрээр: y = kx + м, Хаана .

Энэ тэгшитгэлийн шийдэл буюу үндэс нь дараах хос хувьсагчийн утгууд юм (x;y), энэ нь түүнийг таних тэмдэг болгон хувиргадаг. 2 хувьсагчтай шугаман тэгшитгэл нь эдгээр шийдүүдийн хязгааргүй тооны (үндэс) байна. Энэ тэгшитгэлийн геометрийн загвар (график) нь шулуун шугам юм y=kx+m.

Хэрэв тэгшитгэл нь x квадратыг агуулж байвал тэгшитгэлийг дуудна

Бид тэгш байдлын тухай ойлголтыг, тухайлбал тэдгээрийн нэг төрөл болох тоон тэгшитгэлийг судалсны дараа бид өөр нэг чухал төрөл болох тэгшитгэл рүү шилжиж болно. Энэ материалын хүрээнд бид тэгшитгэл, түүний язгуур гэж юу болохыг тайлбарлаж, үндсэн тодорхойлолтуудыг томъёолж, тэгшитгэл, тэдгээрийн үндэсийг олох янз бүрийн жишээг өгөх болно.

Тэгшитгэлийн тухай ойлголт

Ер нь тэгшитгэлийн тухай ойлголтыг сургуулийн алгебрийн хичээлийн эхэнд заадаг. Дараа нь дараах байдлаар тодорхойлогдоно.

Тодорхойлолт 1

Тэгшитгэлолох шаардлагатай үл мэдэгдэх тоо бүхий тэгшитгэл гэж нэрлэдэг.

Үл мэдэгдэх зүйлийг жижиг латин үсгээр, жишээлбэл, t, r, m гэх мэтээр тэмдэглэх нь заншилтай байдаг ч x, y, z ихэвчлэн ашиглагддаг. Өөрөөр хэлбэл, тэгшитгэл нь түүний бичлэгийн хэлбэрээр тодорхойлогддог, өөрөөр хэлбэл тэгшитгэл нь тодорхой хэлбэрт буурсан тохиолдолд л тэгшитгэл болно - энэ нь үсэг, олох ёстой утгыг агуулсан байх ёстой.

Хамгийн энгийн тэгшитгэлийн зарим жишээг өгье. Эдгээр нь x = 5, y = 6 гэх мэт хэлбэрийн тэгшитгэлүүд байж болно, түүнчлэн арифметик үйлдлүүд, жишээлбэл, x + 7 = 38, z − 4 = 2, 8 t = 4, 6: x = 3.

Хаалтны тухай ойлголтыг сурсны дараа хаалттай тэгшитгэлийн тухай ойлголт гарч ирнэ. Үүнд 7 · (x − 1) = 19, x + 6 · (x + 6 · (x − 8)) = 3 гэх мэт. Олдох шаардлагатай үсэг нь нэгээс олон удаа гарч ирж болно, гэхдээ хэд хэдэн удаа, жишээ нь: , жишээ нь, тэгшитгэлд x + 2 + 4 · x − 2 − x = 10 . Мөн үл мэдэгдэх нь зөвхөн зүүн талд төдийгүй баруун талд эсвэл хоёр хэсэгт нэгэн зэрэг байрлаж болно, жишээлбэл, x (8 + 1) − 7 = 8, 3 - 3 = z + 3 эсвэл 8 x. − 9 = 2 (x + 17) .

Цаашилбал, оюутнууд бүхэл тоо, реал, рационал, натурал тоо, түүнчлэн логарифм, үндэс, зэрэглэлийн ойлголтуудтай танилцсаны дараа эдгээр бүх объектыг багтаасан шинэ тэгшитгэлүүд гарч ирдэг. Бид ийм илэрхийллийн жишээнүүдэд тусдаа өгүүллийг зориулав.

7-р ангийн сургалтын хөтөлбөрт хувьсагчийн тухай ойлголт анх удаа гарч байна. Эдгээр нь өөр өөр утгатай үсэг юм (дэлгэрэнгүй мэдээллийг тоон, үсэг, хувьсах илэрхийллийн тухай өгүүллээс үзнэ үү). Энэ үзэл баримтлалд үндэслэн бид тэгшитгэлийг дахин тодорхойлж болно:

Тодорхойлолт 2

Тэгшитгэлутгыг нь тооцох шаардлагатай хувьсагчийг хамарсан тэгшитгэл юм.

Жишээлбэл, x + 3 = 6 x + 7 илэрхийлэл нь x хувьсагчтай тэгшитгэл, 3 y − 1 + y = 0 нь у хувьсагчтай тэгшитгэл юм.

Нэг тэгшитгэл нь нэгээс олон хувьсагчтай байж болох ч хоёр ба түүнээс дээш хувьсагчтай байж болно. Тэдгээрийг хоёр, гурван хувьсагч гэх мэт тэгшитгэл гэж нэрлэдэг. Тодорхойлолтыг бичье.

Тодорхойлолт 3

Хоёр (гурав, дөрөв ба түүнээс дээш) хувьсагчтай тэгшитгэлүүд нь харгалзах тооны үл мэдэгдэх тоог агуулсан тэгшитгэл юм.

Жишээлбэл, 3, 7 · x + 0, 6 = 1 хэлбэрийн тэгшитгэл нь нэг x хувьсагчтай тэгшитгэл, x − z = 5 нь x ба z хоёр хувьсагчтай тэгшитгэл юм. Гурван хувьсагчтай тэгшитгэлийн жишээ нь x 2 + (y − 6) 2 + (z + 0, 6) 2 = 26 болно.

Тэгшитгэлийн үндэс

Тэгшитгэлийн тухай ярихад түүний язгуурын тухай ойлголтыг тодорхойлох хэрэгцээ нэн даруй гарч ирдэг. Энэ нь юу гэсэн үг болохыг тайлбарлахыг хичээцгээе.

Жишээ 1

Бидэнд нэг хувьсагчийг багтаасан тодорхой тэгшитгэл өгөгдсөн. Хэрэв бид үл мэдэгдэх үсгийн оронд тоог орлуулах юм бол тэгшитгэл нь тоон тэгшитгэл болно - үнэн эсвэл худал. Хэрэв тэгшитгэлийн a + 1 = 5 бол үсгийг 2 тоогоор сольвол тэгшитгэл худал болж, 4 бол зөв тэгшитгэл нь 4 + 1 = 5 болно.

Хувьсагч нь жинхэнэ тэгш байдал болж хувирах утгуудыг бид илүү их сонирхож байна. Тэдгээрийг үндэс буюу шийдэл гэж нэрлэдэг. Тодорхойлолтыг бичье.

Тодорхойлолт 4

Тэгшитгэлийн үндэсӨгөгдсөн тэгшитгэлийг жинхэнэ тэгшитгэл болгон хувиргах хувьсагчийн утгыг тэд гэж нэрлэдэг.

Үндэсийг мөн шийдэл гэж нэрлэж болно, эсвэл эсрэгээр - эдгээр хоёр ойлголт нь ижил утгатай.

Жишээ 2

Энэ тодорхойлолтыг тодруулахын тулд жишээ татъя. Дээр бид a + 1 = 5 тэгшитгэлийг өгсөн. Тодорхойлолтын дагуу энэ тохиолдолд язгуур нь 4 байх болно, учир нь үсгийн оронд орлуулснаар энэ нь зөв тоон тэгшитгэлийг өгдөг бөгөөд 2 + 1 = 5 буруу тэгшитгэлтэй тохирч байгаа тул хоёр нь шийдэл болохгүй.

Нэг тэгшитгэл хэдэн үндэстэй байж болох вэ? Тэгшитгэл бүр үндэстэй юу? Эдгээр асуултад хариулъя.

Нэг үндэсгүй тэгшитгэлүүд бас байдаг. Жишээ нь 0 x = 5 байх болно. Бид түүнд хязгааргүй олон тооны өөр тоог орлуулж болох боловч 0-ээр үржүүлэхэд үргэлж 0 гарч ирдэг тул тэдгээрийн аль нь ч үүнийг жинхэнэ тэгшитгэл болгон хувиргахгүй.

Мөн хэд хэдэн үндэстэй тэгшитгэлүүд байдаг. Тэд төгсгөлтэй эсвэл хязгааргүй тооны үндэстэй байж болно.

Жишээ 3

Тэгэхээр x − 2 = 4 тэгшитгэлд зөвхөн нэг язгуур байна - зургаа, x 2 = 9-д хоёр үндэс - гурав ба хасах гурав, x -д · (x - 1) · (x - 2) = 0 гурван үндэс - тэг, нэг, хоёр, x=x тэгшитгэлд хязгааргүй олон үндэс бий.

Одоо тэгшитгэлийн язгуурыг хэрхэн зөв бичихийг тайлбарлая. Хэрэв байхгүй бол бид "тэгшитгэлд үндэс байхгүй" гэж бичнэ. Энэ тохиолдолд та хоосон олонлогийн ∅ тэмдгийг бас зааж болно. Хэрэв үндэс байгаа бол бид тэдгээрийг таслалаар тусгаарлаж бичнэ эсвэл буржгар хаалтанд оруулан багцын элемент болгон зааж өгнө. Тиймээс, хэрэв тэгшитгэл нь 2, 1, 5 гэсэн гурван үндэстэй бол бид 2, 1, 5 эсвэл (- 2, 1, 5) гэж бичнэ.

Үндэсийг энгийн тэгш байдлын хэлбэрээр бичихийг зөвшөөрнө. Тэгэхээр тэгшитгэл дэх үл мэдэгдэхийг у үсгээр тэмдэглэж, язгуур нь 2 ба 7 байвал у = 2 ба у = 7 гэж бичнэ. Заримдаа үсгүүдэд доод тэмдэгтүүдийг нэмдэг, жишээлбэл, x 1 = 3, x 2 = 5. Ийм байдлаар бид язгууруудын тоог зааж өгдөг. Хэрэв тэгшитгэл нь хязгааргүй тооны шийдэлтэй бол бид хариултыг тоон интервал хэлбэрээр бичих эсвэл нийтээр хүлээн зөвшөөрөгдсөн тэмдэглэгээг ашиглана: натурал тоонуудын багцыг N, бүхэл тоо - Z, бодит тоо - R гэж тэмдэглэнэ. Хэрэв тэгшитгэлийн шийд нь дурын бүхэл тоо байх шаардлагатай бол x ∈ Z, нэгээс ес хүртэлх бодит тоо байвал у ∈ 1, 9 гэж бичнэ гэж бодъё.

Хэрэв тэгшитгэл нь хоёр, гурав ба түүнээс дээш үндэстэй бол бид дүрмээр бол үндэс биш, харин тэгшитгэлийн шийдлийн талаар ярьдаг. Хэд хэдэн хувьсагчтай тэгшитгэлийн шийдийн тодорхойлолтыг томъёолъё.

Тодорхойлолт 5

Хоёр, гурав ба түүнээс дээш хувьсагчтай тэгшитгэлийн шийдэл нь өгөгдсөн тэгшитгэлийг зөв тоон тэгшитгэл болгон хувиргах хувьсагчийн хоёр, гурав ба түүнээс дээш утгууд юм.

Тодорхойлолтыг жишээгээр тайлбарлая.

Жишээ 4

Хоёр хувьсагчтай тэгшитгэл болох x + y = 7 илэрхийлэл байна гэж бодъё. Эхний оронд нэгийг, хоёр дахь оронд хоёрыг орлъё. Бид буруу тэгшитгэл авах бөгөөд энэ нь хос утгууд нь энэ тэгшитгэлийн шийдэл болохгүй гэсэн үг юм. Хэрэв бид 3 ба 4-р хосыг авбал тэгш байдал үнэн болох бөгөөд энэ нь бид шийдлийг олсон гэсэн үг юм.

Ийм тэгшитгэл нь үндэсгүй эсвэл хязгааргүй олон байж болно. Хэрэв бид хоёр, гурав, дөрөв ба түүнээс дээш утгыг бичих шаардлагатай бол тэдгээрийг таслалаар тусгаарлан хаалтанд бичнэ. Өөрөөр хэлбэл, дээрх жишээн дээр хариулт нь (3, 4) шиг харагдах болно.

Практикт та ихэвчлэн нэг хувьсагч агуулсан тэгшитгэлтэй харьцах хэрэгтэй болдог. Бид тэдгээрийг шийдвэрлэх алгоритмыг тэгшитгэлийг шийдвэрлэхэд зориулсан нийтлэлд нарийвчлан авч үзэх болно.

Хэрэв та текстэнд алдаа байгааг анзаарсан бол үүнийг тодруулаад Ctrl+Enter дарна уу

Тэгшитгэл гэдэг нь тэгшитгэл болох, үл мэдэгдэхийг агуулсан математик илэрхийлэл юм. Хэрэв тэгш байдал нь түүнд багтсан үл мэдэгдэх бүх зөвшөөрөгдөх утгын хувьд үнэн бол түүнийг ижил төстэй байдал гэж нэрлэдэг; жишээ нь: (x – 1)2 = (x – 1)(x – 1) хэлбэрийн хамаарал нь x-ийн бүх утгуудад тохирно.

Хэрэв үл мэдэгдэх x-г агуулсан тэгшитгэл нь таних тэмдэгтэй адил x-ийн бүх утгуудад биш харин зөвхөн тодорхой х утгуудад тохирч байвал x-ийн утгыг тодорхойлох нь ашигтай байж болох юм. тэгшитгэл хүчинтэй байна. Ийм x утгыг тэгшитгэлийн үндэс буюу шийд гэж нэрлэдэг. Жишээлбэл, 5-ын тоо нь 2x + 7= 17 тэгшитгэлийн үндэс юм.

Тэгшитгэлийн онол гэж нэрлэгддэг математикийн салбарт судалгааны гол сэдэв нь тэгшитгэлийг шийдвэрлэх аргууд юм. Сургуулийн алгебрийн хичээл дээр тэгшитгэлд ихээхэн анхаарал хандуулдаг.

Тэгшитгэлийг судлах түүх олон зууны тэртээгээс эхэлдэг. Тэгшитгэлийн онолыг хөгжүүлэхэд хувь нэмрээ оруулсан хамгийн алдартай математикчид:

Архимед (МЭӨ 287-212 он) бол эртний Грекийн эрдэмтэн, математикч, механикч юм. Куб тэгшитгэл болгон бууруулсан бодлогыг судалж байхдаа Архимед шинж чанарын үүргийг олж нээсэн бөгөөд үүнийг хожим дискриминант гэж нэрлэсэн.

Франсуа Вьет 16-р зуунд амьдарч байжээ. Тэрээр математикийн янз бүрийн асуудлыг судлахад асар их хувь нэмэр оруулсан. Ялангуяа тэрээр тэгшитгэлийн коэффициентүүдийн үсгийн тэмдэглэгээг нэвтрүүлж, квадрат тэгшитгэлийн язгууруудын хооронд холболтыг тогтоожээ.

Леонхард Эйлер (1707 - 1783) - математикч, механикч, физикч, одон орон судлаач. Зохиогч St. Математик анализ, дифференциал тэгшитгэл, геометр, тооны онол, ойролцоо тооцоолол, селестиел механик, математик, оптик, баллистик, хөлөг онгоцны үйлдвэрлэл, хөгжмийн онол гэх мэт 800 гаруй бүтээлүүд нь шинжлэх ухааны хөгжилд ихээхэн нөлөө үзүүлсэн. Тэрээр х хувьсагчийн тригонометрийн функцийг экспоненциал функцээр илэрхийлдэг томъёог (Эйлерийн томъёо) гаргаж авсан.

Лагранж Жозеф Луис (1736 - 1813), Францын математикч, механикч. Тэрээр алгебрийн (тэгшитгэлийн язгуурын тэгш хэмийн функц, дифференциал тэгшитгэлийн онол, тогтмолуудын хувьсах арга) судалгаа зэрэг гайхалтай судалгаа хийсэн.

Ж.Лагранж, А.Вандермонд нар бол Францын математикч юм. 1771 онд тэгшитгэлийн системийг шийдвэрлэх аргыг (орлуулах арга) анх ашигласан.

Гаусс Карл Фридрих (1777 -1855) - Германы математикч. Тэрээр тойрог хуваах тэгшитгэлийн онолыг тодорхойлсон ном бичсэн (өөрөөр хэлбэл xn - 1 = 0 тэгшитгэлүүд) нь олон талаараа Галуагийн онолын үлгэр жишээ болсон юм. Тэрээр эдгээр тэгшитгэлийг шийдвэрлэх ерөнхий аргуудаас гадна тэдгээрийн хоорондын холбоог тогтоож, ердийн олон өнцөгтийг бий болгосон. Эртний Грекийн эрдэмтдээс хойш анх удаа тэрээр энэ асуудалд чухал алхам хийсэн, тухайлбал тэрээр луужин болон захирагчийн тусламжтайгаар ердийн n-гоныг барьж болох n-ийн бүх утгыг олсон. Би нэмэх аргыг судалсан. Тэгшитгэлийн системийг нэмэх, хуваах, үржүүлэх боломжтой гэж би дүгнэсэн.

O. I. Сомов - математикийн янз бүрийн хэсгүүдийг чухал, олон тооны бүтээлээр баяжуулсан бөгөөд тэдгээрийн дунд өндөр түвшний тодорхой алгебрийн тэгшитгэлийн онол багтжээ.

Галуа Эваристе (1811-1832) - Францын математикч. Түүний гол гавьяа бол Ж.Лагранж, Н.Абель болон бусад хүмүүсийн эхлүүлсэн алгебрийн тэгшитгэлийн шийдлийн талаарх судалгааг үргэлжлүүлж, алгебрийн тэгшитгэлийн онолыг бий болгосонтой холбогдуулан олж авсан санааны багцыг томъёолж өгсөн явдал юм. нэг үл мэдэгдэх өндөр зэрэгтэй.

А.В.Погорелов (1919 – 1981) - Түүний ажил нь геометрийн аргуудыг хэсэгчилсэн дифференциал тэгшитгэлийн онолын аналитик аргуудтай хослуулсан. Түүний бүтээлүүд нь шугаман бус дифференциал тэгшитгэлийн онолд чухал нөлөө үзүүлсэн.

П.Руффини - Италийн математикч. Тэрээр орлуулалтын багцын хаалттай байдлыг системтэйгээр ашиглан 5-р зэргийн тэгшитгэлийн шийдэгдэхгүй байдлыг нотлохын тулд хэд хэдэн бүтээлээ зориулжээ.

Эрдэмтэд тэгшитгэлийг удаан хугацаанд судалж байгаа хэдий ч шинжлэх ухаан хүмүүс тэгшитгэлийг хэрхэн, хэзээ ашиглах шаардлагатайг мэдэхгүй байна. Хүмүүс хүн болсон цагаасаа хойш хамгийн энгийн тэгшитгэлийг шийдвэрлэхэд хүргэдэг асуудлыг шийдэж ирсэн нь мэдэгдэж байна. Өөр нэг МЭӨ 3-4 мянган жилийн дараа. д. Египетчүүд, Вавилончууд тэгшитгэлийг хэрхэн шийдэхийг мэддэг байсан. Эдгээр тэгшитгэлийг шийдвэрлэх дүрэм нь орчин үеийнхтэй давхцаж байгаа боловч тэдгээр нь яаж ирсэн нь тодорхойгүй байна.

Эртний Египт, Вавилонд хуурамч байрлалын аргыг хэрэглэж байжээ. Нэг үл мэдэгдэх 1-р зэргийн тэгшитгэлийг үргэлж ax + b = c хэлбэрт буулгаж болно, үүнд a, b, c бүхэл тоонууд байна. Арифметик үйлдлийн дүрмийн дагуу ax = c - b,

Хэрэв b > c бол c b нь сөрөг тоо болно. Сөрөг тоонууд нь египетчүүд болон бусад олон хожмын ард түмэнд мэдэгддэггүй байсан (тэдгээрийг зөвхөн XVII зуунд эерэг тоонуудтай тэнцүү хэмжээгээр математикт ашиглаж эхэлсэн). Бидний одоо нэгдүгээр зэргийн тэгшитгэлээр шийдэж байгаа асуудлыг шийдэхийн тулд худал байрлалын аргыг зохион бүтээжээ. Ахмес папируст 15 асуудлыг ийм аргаар шийддэг. Египетчүүд үл мэдэгдэх тооны тусгай тэмдэгтэй байсан бөгөөд үүнийг саяхныг хүртэл "хэрхэн" гэж уншиж, "овоо" ("овоо" эсвэл "үл мэдэгдэх тоо" нэгж) гэж орчуулдаг байв. Одоо тэд арай бага алдаатай уншдаг: "тийм ээ." Ахмесийн ашигласан шийдлийн аргыг нэг худал байрлалын арга гэж нэрлэдэг. Энэ аргыг ашиглан ax = b хэлбэрийн тэгшитгэлийг шийддэг. Энэ арга нь тэгшитгэлийн тал бүрийг а-д хуваахыг хэлнэ. Үүнийг египетчүүд болон вавилончууд хоёуланг нь ашигладаг байсан. Янз бүрийн ард түмэн хоёр хуурамч албан тушаалын аргыг ашигласан. Арабчууд энэ аргыг механикжуулж, Магнитскийн арифметик зэрэг Европын ард түмний сурах бичигт шилжүүлсэн хэлбэрийг олж авсан. Магнитский уг шийдлийг "хуурамч дүрэм" гэж нэрлээд, энэ аргыг тодорхойлсон номынхоо хэсэгт бичжээ.

Энэ хэсэг нь маш зальтай, учир нь та түүнтэй хамт бүх зүйлийг хийж болно. Иргэншилд байгаа зүйл төдийгүй, мэргэн ухаантнуудын хувьд тэнгэрийн бөмбөрцөгт жагсаагдсан сансар огторгуйн дээд шинжлэх ухаанд ч хэрэгтэй байдаг.

Магнитскийн шүлгийн агуулгыг дараах байдлаар товч дүгнэж болно: арифметикийн энэ хэсэг нь маш төвөгтэй юм. Түүний тусламжтайгаар та өдөр тутмын практикт шаардлагатай зүйлийг тооцоолж зогсохгүй "ухаантай" тулгардаг "дээд" асуултуудыг шийдэж чадна. Магнитский "хуурамч дүрмийг" арабчуудын өгсөн хэлбэрээр ашигладаг бөгөөд үүнийг "хоёр алдааны арифметик" эсвэл "масштабын арга" гэж нэрлэдэг. Энэтхэгийн математикчид ихэвчлэн шүлгээр бодлого гаргадаг. Бадамлянхуа асуудал:

Нам гүм нуурын дээгүүр, уснаас хагас хэмжүүр өндөрт бадамлянхуа цэцгийн өнгө харагдана. Тэр ганцаараа өссөн бөгөөд салхи долгион шиг түүнийг хажуу тийш нь бөхийлгөж, цаашид больжээ

Усан дээгүүр цэцэглэдэг. Загасчны нүд түүнийг өссөн газраасаа хоёр метрийн зайд олжээ. Энд нуурын ус хэр гүн байдаг вэ? Би чамаас асуулт асууя.

Тэгшитгэлийн төрлүүд

Шугаман тэгшитгэл

Шугаман тэгшитгэл нь дараах хэлбэрийн тэгшитгэл юм: ax + b = 0, энд a ба b нь зарим тогтмолууд юм. Хэрэв a нь тэгтэй тэнцүү биш бол тэгшитгэл нь нэг үндэстэй байна: x = - b: a (ax + b; ax = - b; x = - b: a.).

Жишээ нь: шугаман тэгшитгэлийг шийд: 4x + 12 = 0.

Шийдэл: a = 4, b = 12 тул x = - 12: 4; x = - 3.

Шалгах: 4 (- 3) + 12 = 0; 0 = 0.

0 = 0 тул -3 нь анхны тэгшитгэлийн үндэс болно.

Хариулт. x = -3

Хэрэв а нь тэгтэй, b нь тэгтэй тэнцүү бол ax + b = 0 тэгшитгэлийн үндэс нь дурын тоо юм.

Жишээлбэл:

0 = 0. 0 нь 0-тэй тэнцүү тул 0x + 0 = 0 тэгшитгэлийн үндэс нь дурын тоо болно.

Хэрэв a нь тэгтэй тэнцүү, b нь тэгтэй тэнцүү биш бол ax + b = 0 тэгшитгэл нь үндэсгүй болно.

Жишээлбэл:

0 = 6. 0 нь 6-тай тэнцүү биш тул 0x – 6 = 0 нь үндэсгүй болно.

Шугаман тэгшитгэлийн системүүд.

Шугаман тэгшитгэлийн систем нь бүх тэгшитгэлүүд нь шугаман байдаг систем юм.

Системийг шийдэх нь түүний бүх шийдлийг олох гэсэн үг юм.

Шугаман тэгшитгэлийн системийг шийдэхийн өмнө та түүний шийдлийн тоог тодорхойлж болно.

Тэгшитгэлийн системийг өгье: (a1x + b1y = c1, (a2x + b2y = c2).

Хэрэв a1-ийг a2-т хуваасан нь b1-ийг b2-т хуваасантай тэнцүү биш бол систем нэг өвөрмөц шийдэлтэй байна.

Хэрэв a1-ийг a2-т хуваасан нь b1-ийг b2-т хуваасан, харин c1-ийг c2-д хуваасантай тэнцүү бол системд шийдэл байхгүй болно.

Хэрэв a1-ийг a2-т хуваасан нь b1-ийг b2-д хуваасан, c1-ийг c2-д хуваасантай тэнцүү бол систем нь хязгааргүй олон шийдтэй байна.

Дор хаяж нэг шийдэлтэй тэгшитгэлийн системийг нэгэн зэрэг гэж нэрлэдэг.

Тогтмол систем нь хязгаарлагдмал тооны шийдтэй бол тодорхойгүй, шийдлүүдийн олонлог нь хязгааргүй бол тодорхойгүй гэж нэрлэдэг.

Нэг шийдэлгүй системийг үл нийцэх буюу зөрчилтэй гэж нэрлэдэг.

Шугаман тэгшитгэлийг шийдвэрлэх арга

Шугаман тэгшитгэлийг шийдэх хэд хэдэн арга байдаг:

1) Сонгох арга. Энэ бол хамгийн энгийн арга юм. Энэ нь үл мэдэгдэх бүх хүчинтэй утгыг тоолох замаар сонгохоос бүрдэнэ.

Жишээлбэл:

Тэгшитгэлийг шийд.

x = 1. Дараа нь

4 = 6. 4 нь 6-тай тэнцүү биш тул x = 1 гэсэн бидний таамаглал буруу байсан.

x = 2 гэж үзье.

6 = 6. 6 нь 6-тай тэнцүү тул x = 2 гэсэн бидний таамаглал зөв байсан.

Хариулт: x = 2.

2) Хялбаршуулах арга

Энэ арга нь үл мэдэгдэхийг агуулсан бүх нэр томъёог зүүн тал руу, мэдэгдэж буйг нь эсрэг тэмдэгтэй баруун тийш шилжүүлэх, ижил төстэй зүйлийг авчрах, тэгшитгэлийн хоёр талыг үл мэдэгдэх коэффициентээр хуваахаас бүрдэнэ.

Жишээлбэл:

Тэгшитгэлийг шийд.

5х – 4 = 11 + 2х;

5х – 2х = 11 + 4;

3х = 15; : (3) x = 5.

Хариулт. x = 5.

3) График арга.

Энэ нь өгөгдсөн тэгшитгэлийн функцүүдийн графикийг бүтээхээс бүрдэнэ. Шугаман тэгшитгэлд y = 0 байх тул график нь у тэнхлэгтэй параллель байх болно. Графикийн х тэнхлэгтэй огтлолцох цэг нь энэ тэгшитгэлийн шийдэл болно.

Жишээлбэл:

Тэгшитгэлийг шийд.

y = 7. Дараа нь y = 2x + 3 болно.

Хоёр тэгшитгэлийн функцийг зуръя:

Шугаман тэгшитгэлийн системийг шийдвэрлэх арга

Долдугаар ангид тэд тэгшитгэлийн системийг шийдэх гурван аргыг судалдаг.

1) Орлуулах арга.

Энэ арга нь тэгшитгэлийн аль нэгэнд үл мэдэгдэх нэгийг нөгөөгөөр илэрхийлэхэд оршино. Үүссэн илэрхийлэл нь өөр тэгшитгэлд орлуулж, дараа нь нэг үл мэдэгдэх тэгшитгэл болж, дараа нь шийдэгдэнэ. Энэхүү үл мэдэгдэхийн үр дүнгийн утгыг анхны системийн дурын тэгшитгэлд орлуулж, хоёр дахь үл мэдэгдэх утгыг олно.

Жишээлбэл.

Тэгшитгэлийн системийг шийд.

5x - 2y - 2 = 1.

3x + y = 4; y = 4 - 3x.

Үр дүнгийн илэрхийлэлийг өөр тэгшитгэлд орлъё:

5х – 2(4 – 3х) -2 = 1;

5x – 8 + 6x = 1 + 2;

11x = 11; : (11) x = 1.

Гарсан утгыг 3x + y = 4 тэгшитгэлд орлъё.

3 1 + y = 4;

3 + y = 4; y = 4 – 3; y = 1.

Шалгалт.

/3 1 + 1 = 4,

\5 · 1 – 2 · 1 – 2 = 1;

Хариулт: x = 1; y = 1.

2) Нэмэх арга.

Энэ арга нь хэрэв өгөгдсөн систем нь гишүүн бүлгүүдийг нэмэхэд нэг үл мэдэгдэх тэгшитгэл үүсгэдэг тэгшитгэлээс бүрддэг бол энэ тэгшитгэлийг шийдсэнээр бид үл мэдэгдэх аль нэгийн утгыг олж авна. Энэхүү үл мэдэгдэхийн үр дүнгийн утгыг анхны системийн дурын тэгшитгэлд орлуулж, хоёр дахь үл мэдэгдэх утгыг олно.

Жишээлбэл:

Тэгшитгэлийн системийг шийд.

/3у – 2х = 5,

\5x – 3y = 4.

Үүссэн тэгшитгэлийг шийдье.

3х = 9; : (3) x = 3.

Гарсан утгыг 3y – 2x = 5 тэгшитгэлд орлъё.

3у – 2 3 = 5;

3у = 11; : (3) y = 11/3; у = 3 2/3.

Тэгэхээр x = 3; у = 3 2/3.

Шалгалт.

/3 11/3 – 2 3 = 5,

\5 · 3 – 3 · 11/ 3 = 4;

Хариулт. x = 3; у = 3 2/3

3) График арга.

Энэ арга нь тэгшитгэлийг нэг координатын системд зурахад суурилдаг. Хэрэв тэгшитгэлийн графикууд огтлолцдог бол огтлолцлын цэгийн координатууд нь энэ системийн шийдэл болно. Хэрэв тэгшитгэлийн графикууд нь зэрэгцээ шугамууд байвал энэ системд шийдэл байхгүй болно. Хэрэв тэгшитгэлийн графикууд нэг шулуун шугамд нийлбэл систем хязгааргүй олон шийдтэй байна.

Жишээлбэл.

Тэгшитгэлийн системийг шийд.

18x + 3y - 1 = 8.

2x - y = 5; 18x + 3y - 1 = 8;

Y = 5 - 2x; 3y = 9 - 18x; : (3) y = 2x - 5. y = 3 - 6x.

y = 2x - 5, y = 3 - 6x функцуудын графикийг ижил координатын систем дээр байгуулъя.

y = 2x - 5 ба y = 3 - 6x функцуудын графикууд А цэг дээр огтлолцоно (1; -3).

Иймд энэ тэгшитгэлийн системийн шийдэл нь x = 1, y = -3 болно.

Шалгалт.

2 1 - (- 3) = 5,

18 1 + 3 (-3) - 1 = 8.

18 - 9 – 1 = 8;

Хариулт. x = 1; y = -3.

Дүгнэлт

Дээр дурдсан бүх зүйл дээр үндэслэн тэгшитгэл нь орчин үеийн ертөнцөд зөвхөн практик асуудлыг шийдвэрлэхэд төдийгүй шинжлэх ухааны хэрэгсэл болгон шаардлагатай гэж дүгнэж болно. Тийм ч учраас олон эрдэмтэд энэ асуудлыг судалж, үргэлжлүүлэн судалж байна.

Алгебрийн тэгшитгэлийн төрөл, тэдгээрийг шийдвэрлэх арга

Математик сонирхдог оюутнуудын хувьд өндөр зэрэглэлийн алгебрийн тэгшитгэлийг шийдвэрлэхдээ үндсийг хурдан олох, үлдэгдлийг x -  буюу сүх + b хоёрт хуваах үр дүнтэй арга бол Хорнер схем юм.

Хорнерын схемийг авч үзье.

P(x)-ийг х – -д хуваахдаа бүрэн бус хэсгийг тэмдэглэе.

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, үлдэгдэл нь b n байна.

P(x) = Q (x)(x–) + b n тул тэгш байдал биелнэ.

a 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х– ) + b n

Баруун талын хаалтуудыг нээж, зүүн ба баруун талд байгаа х-ийн ижил зэрэглэлийн коэффициентүүдийг харьцуулж үзье. a 0 = b 0 ба 1  k  n-ийн хувьд a k = b k -  b k -1 хамаарал биелнэ. Эндээс b 0 = a 0 ба b k = a k +  b k -1, 1  k  n болно.

Бид олон гишүүнт Q (x) ба үлдсэн b n-ийн коэффициентүүдийн тооцоог хүснэгт хэлбэрээр бичнэ.

a 0

a 1

a 2

А n-1

А n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Жишээ 1. 2x 4 – 7x 3 – 3x 2 + 5x – 1 олон гишүүнтийг x + 1-д хуваа.

Шийдэл. Бид Хорнерын схемийг ашигладаг.

2x 4 – 7x 3 – 3x 2 + 5x – 1-ийг x + 1-д хуваахад бид 2x 3 – 9x 2 + 6x – 1 болно.

Хариулт: 2 x 3 – 9x 2 + 6x – 1

Жишээ 2. P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1 байх P(3)-ийг тооцоол.

Шийдэл. Безутын теорем ба Хорнерын схемийг ашиглан бид дараахь зүйлийг олж авна.

Хариулт: P(3) = 535

Дасгал хийх

Хорнерын диаграммыг ашиглан олон гишүүнтийг хуваа

4x + 2 дээр x 3 – x 5 + 132 – 8x 2;

2) Олон гишүүнтийг хуваа

2x 2 – 3x 3 – x + x 5 + 1 дээр x + 1;

3) x = 7 бол P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 олон гишүүнтийн утгыг ол.

1.1. Бүхэл тооны коэффициент бүхий тэгшитгэлийн рационал язгуурыг олох

Бүхэл тоон коэффициент бүхий алгебрийн тэгшитгэлийн рационал язгуурыг олох аргыг дараах теоремоор өгөв.

Теорем:Хэрэв бүхэл тоон коэффициент бүхий тэгшитгэл нь оновчтой үндэстэй бол тэдгээр нь чөлөөт гишүүний хуваагчийг тэргүүлэх коэффициентийн хуваагчаар хуваах коэффициент юм.

Нотолгоо: a 0 x n + a 1 x n -1 + … + a n = 0

x = p/ байг q нь рационал үндэс, q, p нь хоёрдогч.

Тэгшитгэлд p/q бутархайг орлуулж, хуваагчаас чөлөөлөгдөхөд бид олж авна.

a 0 r n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

(1)-ийг хоёр аргаар дахин бичье:

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

a 0 r n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

Тэгш тэгшитгэлээс (2) a n q n нь p-д хуваагддаг ба үүнээс хойш q n ба p нь хоёрдогч, тэгвэл a n нь p-д хуваагдана. Үүний нэгэн адил тэгш байдал (3)-аас 0 нь q-д хуваагдана гэсэн үг. Теорем нь батлагдсан.

Жишээ 1. 2x 3 – 7x 2 + 5x – 1 = 0 тэгшитгэлийг шийд.

Шийдэл. Тэгшитгэлд бүхэл язгуур байхгүй, бид тэгшитгэлийн оновчтой язгуурыг олдог. Тэгшитгэлийн язгуур нь p /q бууруулж болохгүй бутархай байг, тэгвэл чөлөөт гишүүний хуваагчдаас p нь олддог, өөрөөр хэлбэл.  1 тоонуудын дунд, тэргүүлэгч коэффициентийн эерэг хуваагчдын дунд q: 1; 2.

Тэдгээр. тэгшитгэлийн рационал язгуурыг  1,  1/2 тоонуудын дундаас хайх ёстой, P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1) гэж тэмдэглэнэ.  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 нь тэгшитгэлийн үндэс юм.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

Бид авах: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2х – 1)(х 2 – 3х + 1) = 0.

Хоёрдахь хүчин зүйлийг тэгтэй тэнцүүлж, тэгшитгэлийг шийдвэл бид олж авна

Хариулт:
,

Дасгал

Тэгшитгэлийг шийдэх:

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Харилцан тэгшитгэл ба шийдвэрлэх арга

Тодорхойлолт.Үл мэдэгдэх бүхэл тоон хүчин чадалтай тэгшитгэлийг зүүн талын төгсгөлөөс ижил зайд орших коэффициентүүд нь хоорондоо тэнцүү бол харилцан адилгүй гэж нэрлэдэг. хэлбэрийн тэгшитгэл

А x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Сондгой зэрэглэлийн харилцан тэгшитгэл

А x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

үргэлж x = – 1 язгууртай. Иймд x + 1 = 0 ба  x 2 n +  x 2 n -1 + … +  x +  = 0 тэгшитгэлийг нэгтгэсэнтэй тэнцүү. Сүүлийн тэгшитгэл нь a. тэгш хэмтэй харилцан тэгшитгэл. Тиймээс аль ч зэрэгтэй харилцан тэгшитгэлийг шийдэх нь тэгш хэмтэй харилцан адилгүй тэгшитгэлийг шийдвэрлэхэд хүргэдэг.

Үүнийг хэрхэн шийдвэрлэх вэ? Тэгш зэрэгтэй харилцан тэгшитгэл өгье

А x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

x = 0 нь тэгшитгэлийн үндэс биш гэдгийг анхаарна уу. Дараа нь бид тэгшитгэлийг x n-д хуваавал бид олж авна

А x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

Бид зүүн талын нөхцлүүдийг хосоор нь бүлэглэдэг

А( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1 ) + e = 0

Бид x + x -1 = y орлуулалтыг хийнэ. x 2 + x -2 = y 2 – 2 илэрхийллүүдийг орлуулсны дараа;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 тэгшитгэлд бид тэгшитгэлийг авна. цагтАу n + By n -1 +Cy n -2 + … + Ey + D = 0.

Энэ тэгшитгэлийг шийдэхийн тулд та x + x -1 = y k хэлбэрийн хэд хэдэн квадрат тэгшитгэлийг шийдэх хэрэгтэй, энд k = 1, 2, ... n байна. Тиймээс бид анхны тэгшитгэлийн үндсийг олж авна.

Жишээ 1. x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0 тэгшитгэлийг шийд.

Шийдэл. x = – 1 нь тэгшитгэлийн үндэс юм. Хорнерын схемийг хэрэгжүүлье.

Бидний тэгшитгэл дараах хэлбэртэй байна.

(x + 1)(x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Бүлэглэснээр бид дараахь зүйлийг авна.

Орлуулахыг танилцуулъя:
;
;
.

Бид харьцангуй авдаг цагттэгшитгэл: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) – 9 (y + 1) = 0; (y + 1)(y 2 – 9); y 1 = -1, y 2,3 =  3.

Тэгшитгэл шийдвэрлэх
,
,
,

Бид үндсийг нь авдаг:
,
,
,

Хариулт: x 1 = -1,
,

Дасгал

Тэгшитгэлийг шийдэх.

2х 5 + 5х 4 – 13х 3 – 13х 2 + 5х + 2 = 0;

2х 4 + 3х 3 – 16х 2 + 3х + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Тэгшитгэлийг шийдвэрлэх хувьсагчийг орлуулах арга

Хувьсах солих арга нь хамгийн түгээмэл арга юм. Хувьсагчийн өөрчлөлт хийх урлаг нь аль өөрчлөлт нь хамгийн их утга учиртай болохыг, амжилтанд илүү хурдан хүргэхийг харах явдал юм.

Хэрэв тэгшитгэл өгөгдсөн бол

F(f(x)) = 0, (1)

дараа нь үл мэдэгдэх y = f (x) -ийг орлуулснаар эхлээд тэгшитгэлд буурна

F(y) = 0, (2)

дараа нь (2) y 1, y 2, ..., y n, ... тэгшитгэлийн бүх шийдийг олсны дараа f (x) = y 1, f (x) = y 2 тэгшитгэлийн багцыг шийдвэрлэх хүртэл бууруулна. ,..., f (x) = y 2,...

Хувьсагчийг орлуулах аргыг хэрэгжүүлэх үндсэн арга замууд нь:

бутархайн үндсэн шинж чанарыг ашиглах;

биномийн квадратыг тодруулах;

тэгшитгэлийн системд шилжих;

хаалтуудыг хосоор нь нээх;

хашилтыг хосоор нь нээж, тэгшитгэлийн хоёр талыг хуваах;

тэгшитгэлийн зэргийг бууруулах;

давхар солих.

1.3.1. Тэгшитгэлийн хүчийг багасгах

(x 2 + x + 2)(x 2 + x + 3) = 6 (3) тэгшитгэлийг шийд.

Шийдэл. x 2 + x + 2 = y гэж тэмдэглээд дараа нь y (y + 1) = 6-г авч, сүүлчийнхийг нь шийдээд у 1 = 2, y 2 = -3 болно. Энэ тэгшитгэл (3) нь x 2 + x + 2 = 2 тэгшитгэлийн багцтай тэнцүү байна.

x 2 + x + 2 = -3

Эхнийхийг шийдэж, бид x болно 1 = 0, x 2 = -1. Хоёрдахь асуудлыг шийдэж, бид олж авна
,

Хариулт: x 1 = 0, x 2 = -1,

1.3.2. (x + a) (x +) хэлбэрийн дөрөв дэх зэрэглэлийн тэгшитгэлб )(x + в )(x + г ) = м , Энд a + b = c + d, эсвэл a + c = b + d, эсвэл a + d = b + c.

Жишээ. (x - 1)(x - 7)(x -4)(x + 2) = 40 тэгшитгэлийг шийд.

Шийдэл. – 1- 4 = - 7 + 2, - 5 = - 5, эдгээр хос хаалтуудыг үржүүлбэл (x 2 - 5x - 14) (x 2 - 5x + 4) = 40 тэгшитгэлийг авна.

Орлуулахыг танилцуулъя: x 2 - 5x – 14 = y, y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0 тэгшитгэлийг авна. y 1 = -20, y. 2 = 2. Анхны хувьсагч руу буцаж очоод бид тэгшитгэлийн багцыг шийднэ.

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3.4 =

Хариулт: x 1 = 2; x 2 = 3 x 3.4 =

1.3.3. (x + a)(x + b)(x + c)(x + d) = Ex 2 хэлбэрийн тэгшитгэл,

Хаана ab = cd, эсвэл ac =bd, эсвэл ad = bc. Хаалтыг хосоор нь нээж, хоёр хэсгийг х 2  0-д хуваана.

Жишээ. (x - 1)(x - 2)(x - 8)(x - 4) = 4х 2

Шийдэл. Эхний болон гурав дахь, хоёр, дөрөв дэх хаалтанд байгаа тоонуудын үржвэр тэнцүү байна, i.e. – 8 (- 1) = (- 2)(- 4). Заасан хос хаалтыг үржүүлээд (x 2 - 9x + 8)(x 2 - 6x + 8) = 4x 2 тэгшитгэлийг бичье.

x = 0 нь тэгшитгэлийн үндэс биш тул тэгшитгэлийн хоёр талыг х-д хуваана 2  0, бид авна:
, солих:
, анхны тэгшитгэл нь дараах хэлбэртэй байна.т(т+3) =4, т 2 + 3 т=4, т 2 + 3 т – 4=0, т 1 =1, т 2 = - 4.

Анхны хувьсагч руу буцъя:

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

Бид эхний тэгшитгэлийг шийдэж, x-г авна 1,2 = 5 

Хоёр дахь тэгшитгэл нь үндэсгүй.

Хариулт: x 1.2 = 5 

1.3.4. Дөрөв дэх төрлийн тэгшитгэл (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Тэгшитгэл (сүх 2 + б 1 x+ в)(а x 2 + б 2 x + в) = А x 2, энд c  0, А  2
, энэ нь үл мэдэгдэх зүйлийг орлуулсны дараа
дөрвөлжин хэлбэрээр дахин бичих боломжтой бөгөөд амархан шийдэж болно.

Жишээ. (x 2 + x+ 2)(x 2 + 2x + 2) = 2x 2

Шийдэл. Энэ тэгшитгэлийг х-д хувааснаар x = 0 нь энэ тэгшитгэлийн үндэс биш гэдгийг ойлгоход хялбар байдаг. 2 , бид тэгшитгэлийг авна

солих
, бид (y+1)(y+2) = 2 тэгшитгэлийг олж, үүнийг шийдэж, y үндэстэй болно. 1 = 0; 2 цагт = - 3 тул анхны тэгшитгэл нь тэгшитгэлийн багцтай тэнцүү байна

шийдэж, бид x 1 = -1 болно; x 2 = -2.

Хариулт: x 1 = -1; x 2 = -2

1.3.5. Маягтын тэгшитгэл: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

Тэгшитгэл а(cx 2 + х 1 x + q) 2 + б(cx 2 + х 2 x + q) 2 = Сүх 2 хаана а, б, в, q, Аийм байна q 0, А 0, в 0, а 0, б 0 нь x = 0 үндэсгүй тул тэгшитгэлийг х-д хуваана 2 , бид эквивалент тэгшитгэлийг олж авна
, энэ нь сольсны дараа
амархан шийдэгдэх квадрат тэгшитгэл болгон дахин бичиж болно. + 1)( x 2 – 14x + 15 = 0

x 2 – 7 x + 15 = 0

Хариулт: